Numerical Methods > Multiscale methods
During the last decades, multiscale methods have been developed to capture the physics at different scales. Multiscale models are based on the idea of resolving smaller scales, with correct physical models to extract responses that can be used at the macroscopic scale. As an example the Gurson's model is a multiscale homogenization method as it is solving a microscopic problem (plastic flow around the microvoids) to derive a macroscopic homogenized constitutive behavior (the apparent plastic yield surface).
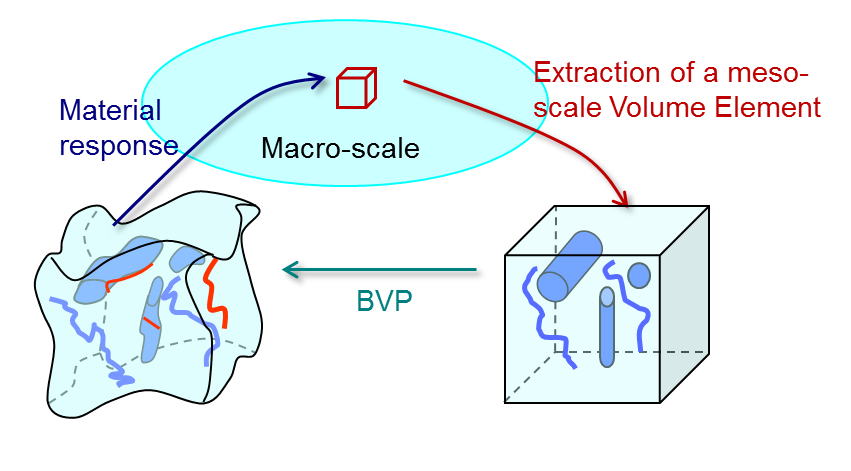
The general idea of a multi-scale method is illustrated in Picture VI.32 in which two boundary value problems (BVP) are solved concurrently:
- The macroscale problem, which is typically the studied structure;
- The mesoscale problem (on a meso-scale Volume Element), which represents the material with its heterogeneities.
The link between the two boundary value problems involves two steps:
- The downscaling: the deformation gradient field is sent from the macroscale to the mesoscale, for example, to define the boundary conditions of the mesoscale BVP;
- The upscaling:the resolution of the mesoscale BVP leads to a homogenized material behavior that can be used at the macroscale.
Multiscale methods assume lengths scale separation, $L_{\text{macro}}>>L_{\text{Volume Element}}>>L_{\text{micro}}$, which is not trivially satisfied in case of failure (but this is beyond the scope of this introduction).
Example: Failure of composite laminates
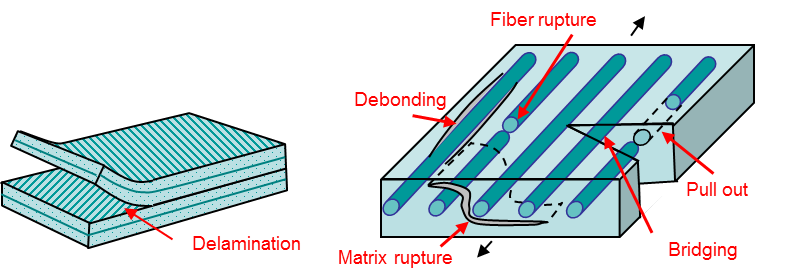
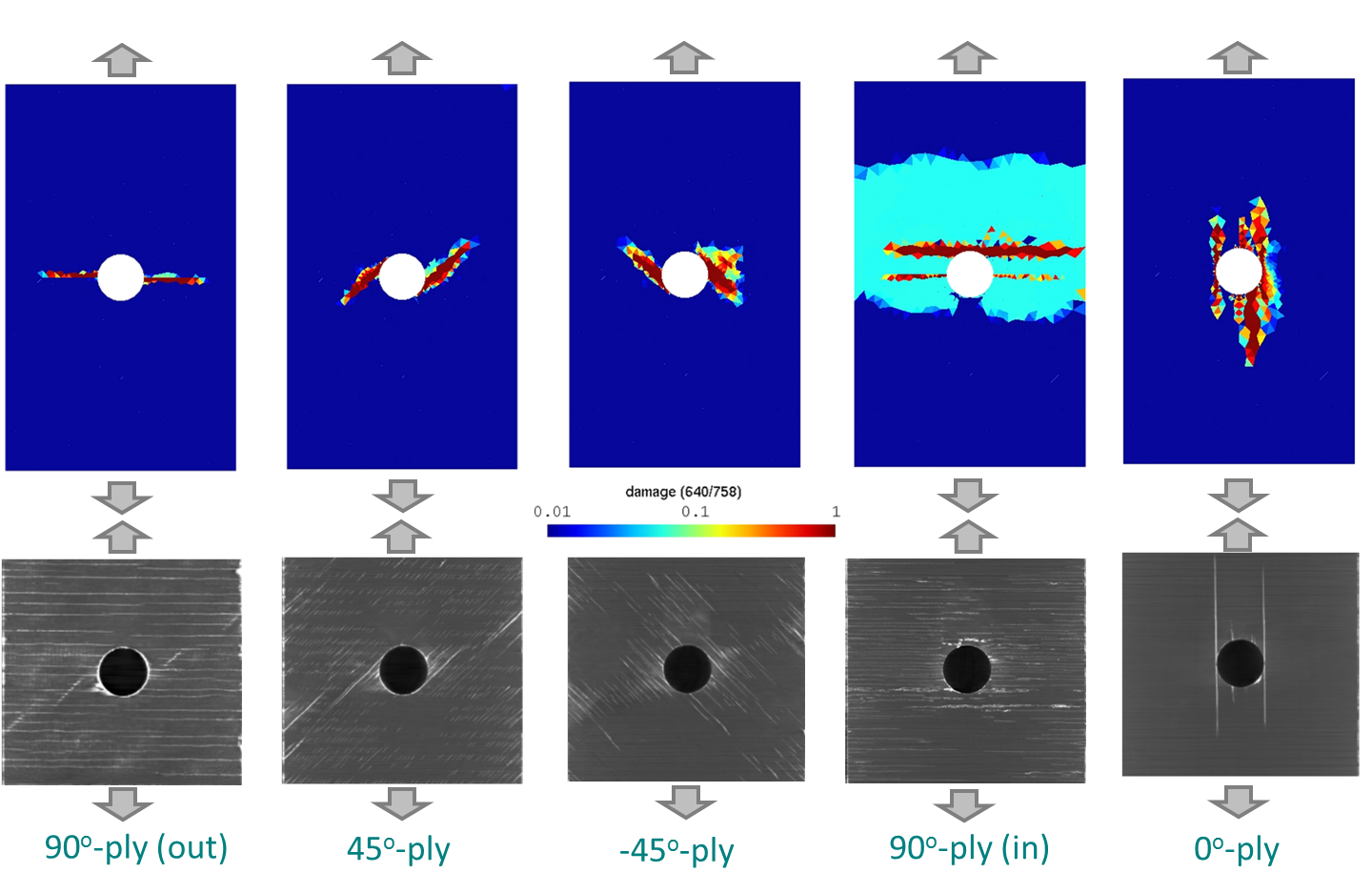
Multiscale models can be used for heterogeneous materials, for which failure involves complex mechanisms, such as composite laminates, see Picture VI.33. An example of application is displayed in Picture VI.34 for the model of the failure of a [$90^o$ / $45^o$ / $-45^o$ / $90^o$ / $0^o$ ] - open hole laminate. In this numerical model:
- Each ply is modeled using a multiscale model embedding a non-local damage model. The different material behaviors of the fibers and of the matrix, the orientation of the fibers ... can thus be accounted for without meshing explicitly the fibers;
- DG-based cohesive elements are used to model the delamination between the plies.
The crack evolution in the different plies is represented by the damage in Picture VI.34, where it can be seen that the numerical model is in good agreement with the experiments.
Example: failure of polycrystalline materials
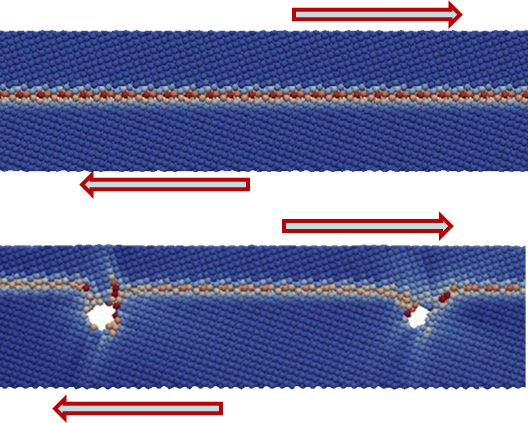
The failure of polycrystalline materials is another example of the multi-scale heterogeneous material study, see Picture VI.35. In this model
- At the macro-scale, the grains are modeled with the finite element method using a crystal plasticity model;
- At the macro-scale, the grain boundaries are modeled using cohesive elements;
- Both the crystal plasticity model and the cohesive law of the cohesive elements are defined using atomistic simulations on meso-scale volume elements, as shown in Picture VI.36.
Such a multiscale model is able to account for the effects of
- The misorientation between the grains, and of the
- Grain size,
on the failure of the polycrystalline structure.