Energetic Approach > Crack that grows straight ahead
We have seen in the previous section that the energy release rate $G$ for any linear elastic materials associated to a crack growth in any directions (mode I, II or III) reads
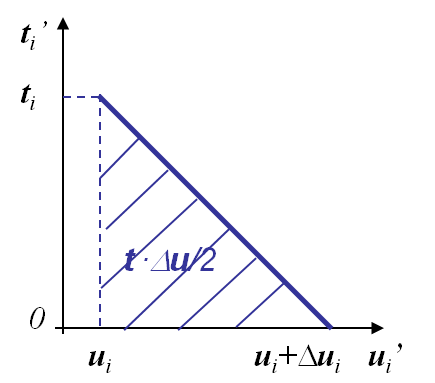
\begin{equation} G= -\partial_A \Delta \Pi_T = - \lim_{\Delta A\rightarrow 0}\frac{1}{\Delta A} \int_{\Delta A}\frac{1}{2} \mathbf{t}\cdot [\![\Delta \mathbf{u} ]\!] d\partial B \label{eq:Glin}, \end{equation}
where
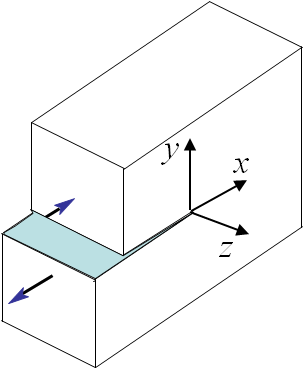
- $\mathbf{t}$ is the tension before crack propagation and where, see Picture III.19,
- $\Delta \mathbf{u}$ is the opening after crack propagation, see Picture III.19.
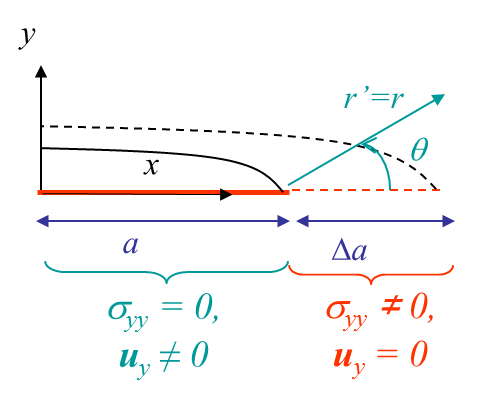
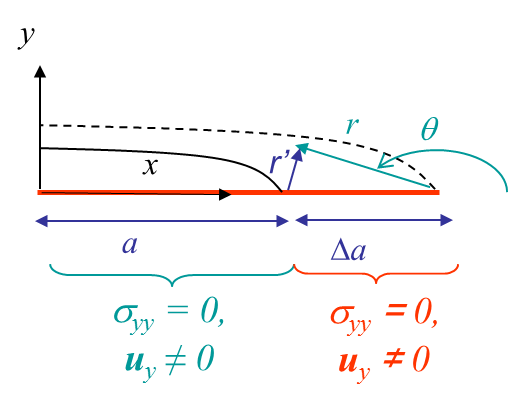
The relation (\ref{eq:Glin}) can be simplified if the crack grows straight ahead as in the case illustrated in Pictures III.20 and III.21. Assuming an increment of fracture surface $\Delta A = t\Delta a$ where $t$ is the thickness along the crack axis, as $A$ has been chosen to be the surface of the positive crack lip $\Delta A^+$, the normal to the crack lip $\mathbf{n}$ is opposite to the $y$-axis, and the surface traction in (\ref{eq:Glin}) simplifies into $\mathbf{t}_i = -\mathbf{\sigma}_{iy}$, leading to
\begin{equation} G= \lim_{\Delta a\rightarrow 0} \frac{1}{\Delta a}\int_0^{\Delta a}\frac{1}{2} \mathbf{\sigma}_{iy}\left(r',\,0\right) [\![\Delta \mathbf{u}_i\left(\Delta a-r',\,\pi\right) ]\!] dr' \label{eq:GlinStraight1}, \end{equation}
where the term in $\mathbf{\sigma}_{iy}$ is the stress before the crack growth and where the term in $\Delta \mathbf{u}_i$ is the resulting displacement jump after the crack growth. In order to evaluate this expression, we consider the different possible loading modes before generalizing to a mixed loading mode.
Energy release rate in mode I (linear elasticity, crack grows straight ahead)
For the 2D mode I loading, only the terms in $i = y$ in (\ref{eq:GlinStraight1}) are considered as $\mathbf{\sigma}_{xy}(r',0) = 0$ ahead of the crack by symmetry. We can now use the asymptotic solution stress and displacement fields
\begin{equation}\begin{cases} \mathbf{\sigma}_{xx} & = & \frac{K_I}{\sqrt{2\pi r}} \cos{\frac{\theta}{2}}\left[1-\sin{\frac{\theta}{2}}\sin{\frac{3\theta}{2}}\right]+\mathcal{O}\left(r^0\right) \\ \mathbf{\sigma}_{yy} &= & \frac{K_I}{\sqrt{2\pi r}} \cos{\frac{\theta}{2}}\left[1+\sin{\frac{\theta}{2}}\sin{\frac{3\theta}{2}}\right]+\mathcal{O}\left(r^0\right)\\ \mathbf{\sigma}_{xy} & = & \frac{K_I}{\sqrt{2\pi r}} \cos{\frac{\theta}{2}}\sin{\frac{\theta}{2}}\cos{\frac{3\theta}{2}}+\mathcal{O}\left(r^0\right)\\ \mathbf{u}_x & = & K_I \frac{1+\nu}{E}\sqrt{\frac{r}{2\pi}} \cos{\frac{ \theta}{2}} \left[\kappa-1+2 \sin^2{\frac{\theta}{2}}\right] +\mathcal{O}\left(r\right)\\ \mathbf{u}_y & = & K_I \frac{1+\nu}{E}\sqrt{\frac{r}{2\pi}}\sin{\frac{ \theta}{2}} \left[\kappa+1-2 \cos^2{\frac{\theta}{2}}\right]+\mathcal{O}\left(r\right)\end{cases},\label{eq:asympModeI} \end{equation}
Before crack growth, the stress field ahead of the crack tip ($\theta = 0$) reads
\begin{equation} \mathbf{\sigma}_{yy}\left(r',\,0\right) = \frac{K_I}{\sqrt{2\pi r'}}. \end{equation}
After crack growth, as the polar referential is linked to the crack tip, we need to change the variable to remain compatible with the previous equation, see Pictures III.20 and III.21. The displacement fields after crack growth on the new crack lips read
\begin{equation} \mathbf{u}_y\left(\Delta a-r',\pm \pi\right) = \pm K_I\frac{\left(1+\nu\right)\left(\kappa+1\right)}{E} \sqrt{\frac{\Delta a -r'}{2\pi}}, \end{equation}
with a "+" sign for the upper lip ($\theta \rightarrow +\pi$) and a "-" sign for the lower lip ($\theta \rightarrow -\pi$). Inserting these stress and displacement fields in (\ref{eq:GlinStraight1}) leads to the following expression of the energy release rate:
\begin{eqnarray} G&=& \lim_{\Delta a\rightarrow 0} \frac{1}{\Delta a}\int_0^{\Delta a}\frac{1}{2} \mathbf{\sigma}_{yy}\left(r',\,0\right) [\![\Delta \mathbf{u}_y\left(\Delta a-r',\,\pi\right) ]\!] dr' \nonumber\\ &=&\lim_{\Delta a\rightarrow 0} \frac{1}{\Delta a}\int_0^{\Delta a}\frac{1}{2} K^2_I\frac{\left(1+\nu\right)\left(\kappa+1\right)}{\pi E} \sqrt{\frac{\Delta a - r'}{r'}} dr' \label{eq:GlinStraight2}. \end{eqnarray}
A sound change of variables $r'=\Delta a \cos^2{x}$ yields
\begin{eqnarray} G & =& \lim_{\Delta a\rightarrow 0} \frac{1}{\Delta a}\int_0^{\frac{\pi}{2}} K^2_I\frac{\left(1+\nu\right)\left(\kappa+1\right)}{ \pi E} \sqrt{\frac{\sin^2 x}{\cos^2 x}} \Delta a \cos x\sin x dx\nonumber \\ &= &\int_0^{\frac{\pi}{2}} K^2_I \frac{\left(1+\nu\right)\left(\kappa+1\right)}{ 2\pi E} \left(1-\cos 2x\right) dx= K^2_I\frac{\left(1+\nu\right)\left(\kappa+1\right)}{4 E}\label{eq:GlinStraight3}.\end{eqnarray}
This last expression can finally be rewritten
\begin{equation} G = \frac{K^2_I}{E'}, \label{eq:modeIG}\end{equation}
where $E'$ depends on the deformation state (through $\kappa$):
- For P-$\sigma$ state: $E' = E$;
- For P-$\varepsilon$ state: $E' = \frac{E}{1-\nu^2}$.
Energy release rate in mode II (linear elasticity, crack grows straight ahead)
For the 2D mode II loading, only the terms in $i = x$ in (\ref{eq:GlinStraight1}) are considered as $\mathbf{\sigma}_{yy}(r',0) = 0$ ahead of the crack by anti-symmetry. We can thus proceed exactly as for mode I, but using the mode II asymptotic solution stress and displacement fields, leading to
\begin{equation} G = \frac{K^2_{II}}{E'}. \label{eq:modeIIG}\end{equation}
Energy release rate in mode III (linear elasticity, crack grows straight ahead)
For the 2D mode III loading, only the terms in $i = z$ in (\ref{eq:GlinStraight1}) are considered as $\mathbf{\sigma}_{xy}(r',0) = 0$ ahead of the crack by symmetry. We can now use the asymptotic solution stress and displacement fields
\begin{equation}\begin{cases} \mathbf{\sigma}_{x z} &=& -\frac{K_{III}}{\sqrt{2 \pi r}} \sin{\frac{\theta}{2}}+\mathcal{O}\left(r^0\right)\\ \mathbf{\sigma}_{y z} &=&\frac{K_{III}}{\sqrt{2 \pi r}} \cos{\frac{\theta}{2}} +\mathcal{O}\left(r^0\right)\\ \mathbf{u}_z &=& \frac{2K_{III}\left(1+\nu\right)}{E} \sqrt{\frac{2r}{\pi}} \sin{\frac{\theta}{2}}+\mathcal{O}\left(r\right)\end{cases}\label{eq:asymptModeIII}. \end{equation}
Thus the stress field ahead of the crack tip, before crack propagation, reads
\begin{equation} \mathbf{\sigma}_{yz}\left(r',\,0\right) = \frac{K_{III}}{\sqrt{2\pi r'}}, \end{equation}
while the displacement fields of the new crack lips after growth read
\begin{equation} \mathbf{u}_z\left(\Delta a-r',\pm \pi\right) = \pm \frac{2 K_{III}\left(1+\nu\right)}{E} \sqrt{2\frac{\Delta a -r'}{\pi}}. \end{equation}
Inserting these stress and displacement field in (\ref{eq:GlinStraight1}) leads to the following expression of the energy release rate:
\begin{eqnarray} G&=& \lim_{\Delta a\rightarrow 0} \frac{1}{\Delta a}\int_0^{\Delta a}\frac{1}{2} \mathbf{\sigma}_{yz}\left(r',\,0\right) [\![\Delta \mathbf{u}_z\left(\Delta a-r',\,\pi\right) ]\!] dr' \nonumber\\&=& \lim_{\Delta a\rightarrow 0} \frac{1}{\Delta a}\int_0^{\Delta a}\frac{1}{2} 4K^2_{III}\frac{\left(1+\nu\right)}{\pi E} \sqrt{\frac{\Delta a - r'}{r'}} dr' \label{eq:GlinStraight4}. \end{eqnarray}
Hence
\begin{equation} G= \frac{K^2_{III}\left(1+\nu\right)}{E}=\frac{K^2_{III}}{2\mu}. \label{eq:modeIIIG} \end{equation}
Energy release rate for general cases
We have now established the relation between the energy release rate and the SIFs for the 3 different loading modes. A few remarks before going further
- The assumptions for these relations to be valid are
- Linear elasticity;
- A crack growing straight ahead.
- Concerning this last assumption, it is questionable to consider a mode II loading as under this condition the crack would probably not grow straight ahead.
With this last concern in mind, we can now consider a mixed loading case. To do so let us consider the initial relation for linear elasticity
\begin{equation} G= \lim_{\Delta a\rightarrow 0} \frac{1}{\Delta a}\int_0^{\Delta a}\frac{1}{2} \mathbf{\sigma}_{iy}\left(r',\,0\right) \left\{\Delta \mathbf{u}_i\left(\Delta a-r',\,\pi\right) \right\} dr'. \end{equation}
When considering the asymptotic solution, it appears that:
- For $i = x$: $\sigma_{xy}(r',0) \neq 0$ and $\mathbf{u}_x(\Delta a-r',\pm \pi) \neq 0$ only for mode II;
- For $i = y$: $\sigma_{yy}(r',0) \neq 0$ and $\mathbf{u}_y(\Delta a-r',\pm \pi) \neq 0$ only for mode I;
- For $i = z$: $\sigma_{yz}(r',0) \neq 0$ and $\mathbf{u}_z(\Delta a-r',\pm \pi) \neq 0$ only for mode III.
As the modes do not interact in the integral, the energies (\ref{eq:modeIG}), (\ref{eq:modeIIG}) and (\ref{eq:modeIIIG}) can be added, leading to
\begin{equation} G = \frac{K^2_I}{E'}+\frac{K^2_{II}}{E'}+\frac{K^2_{III}}{2\mu}. \label{eq:mixedModeG}\end{equation}
Remember: This last expression is only valid for elastic linear materials and for cracks that grow straight ahead! Therefore, what to do when these assumptions are not met? The next page answers this question thanks to the J-Integral concept.