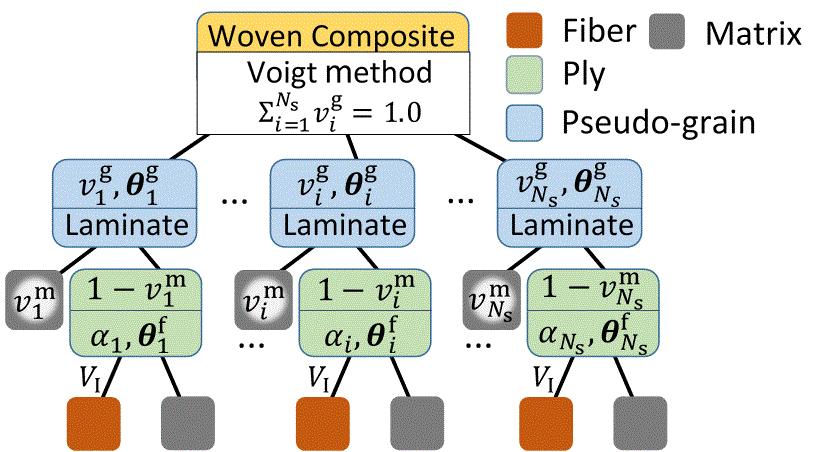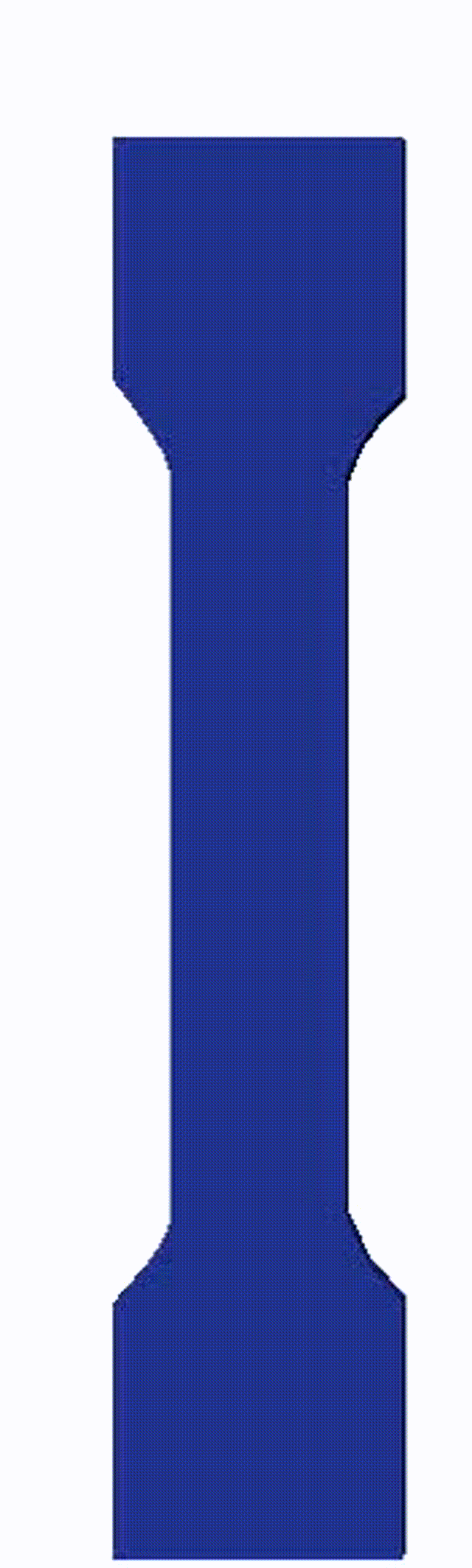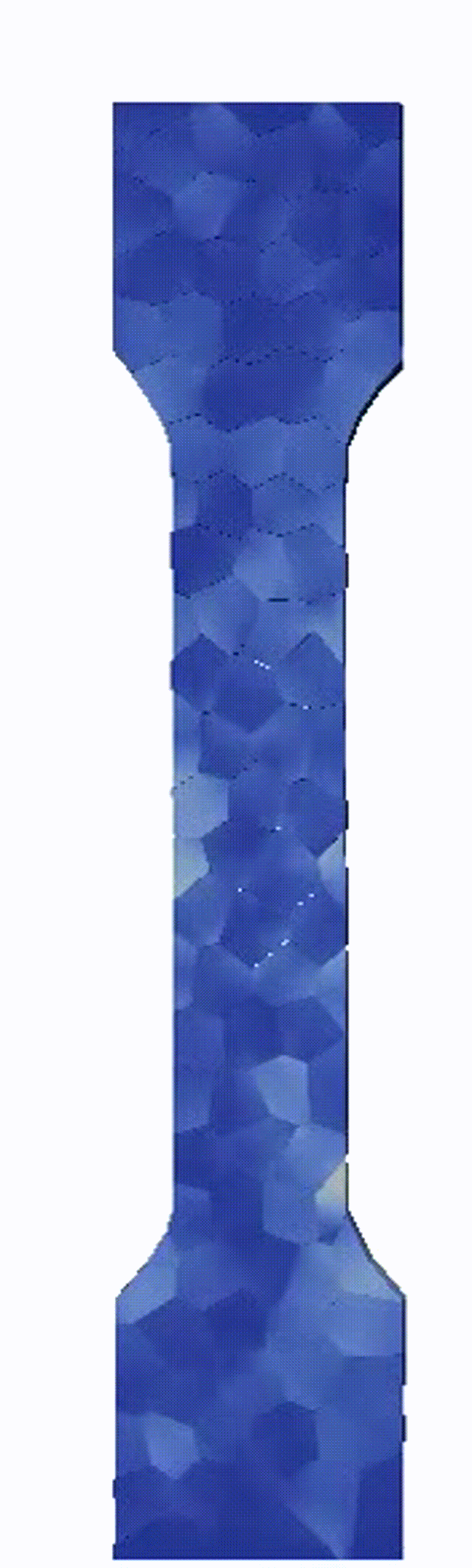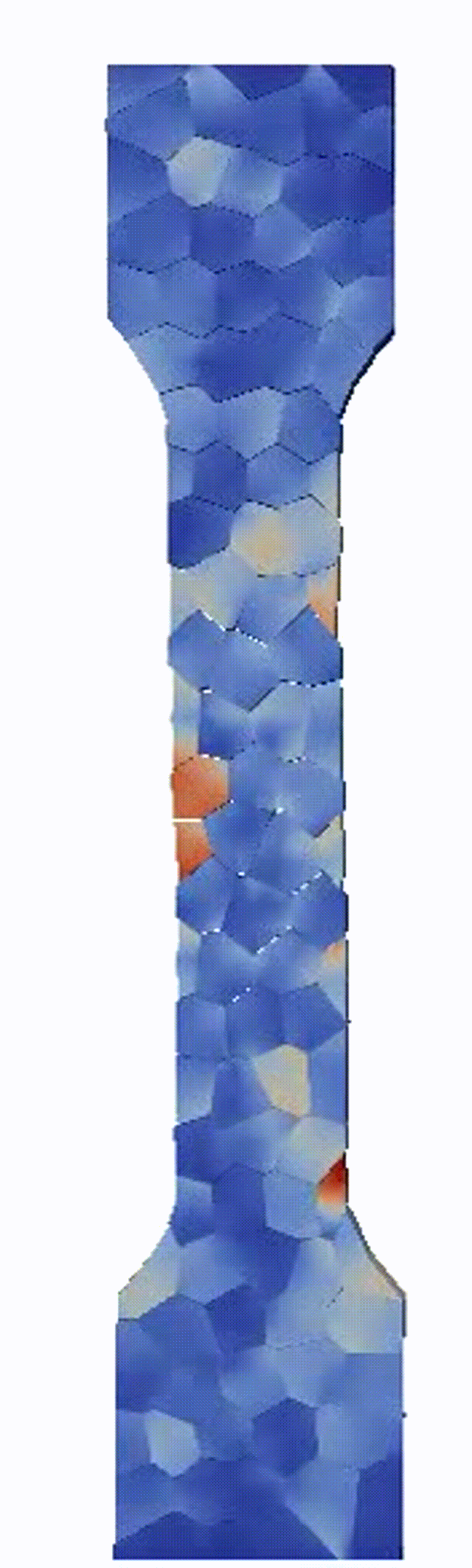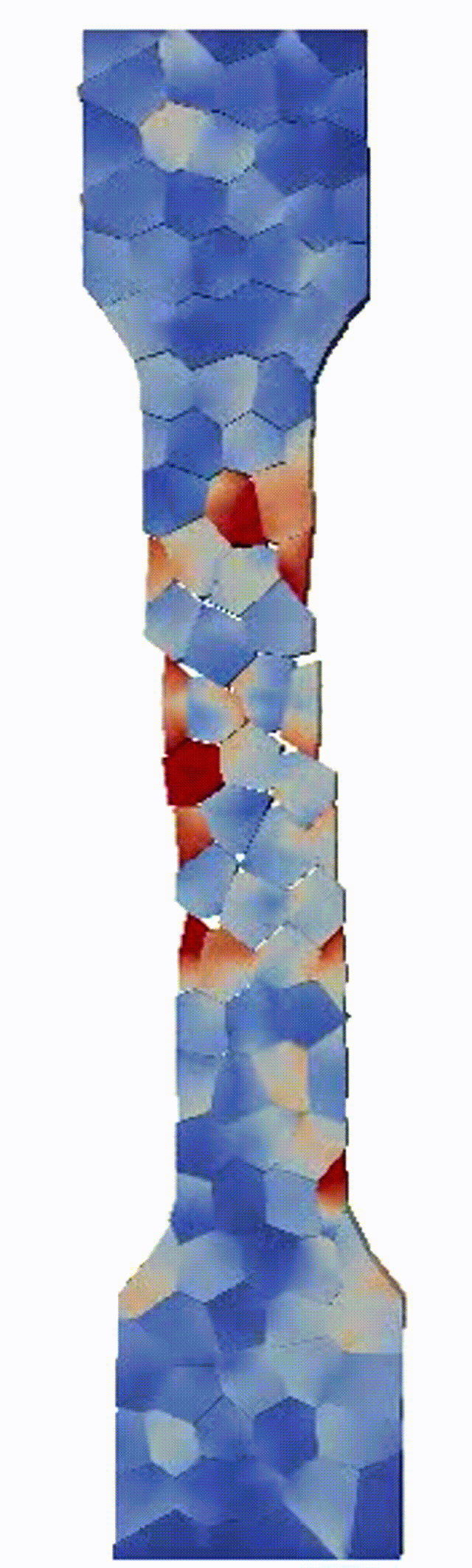Computational & Multiscale Mechanics of Materials
Home | Classes | Research | Open Source Code & Data | Publications | UAV & Aircraft design | Staff
| Quantum Computing | Deep Material Networks | MFH-based Deep Material Networks | Stochastic Deep Material Network | RNN accelerated multi-scale methods | Self-Consistent Reurrent Neural Network | RNN with dimensionality reduction and breakdown | Multi-scale optimisation of meta-materials | Sequential Bayesian Inference of complex model parameters | Bayesian inference of multi-scale models | Microstructural reinforced highly crosslinked epoxy analysis | Finite-strain thermomechanical quasi-nonlinear-viscoelastic viscoplastic model for thermoplastics | Shear & Necking-coalescence for porous models | Ductile failure of High Entropy alloys |Incremental-secant MFH | Instabilities Across the Scales | Second-order Homogenization for metamaterials | Damage-Enhanced MFH | Damage & Phase Field-Enhanced MFH | Stochastic Homogenization of Composite Materials | Stochastic 3-Scale Method for Polycristalline Materials | Stochastic Stiction | Multiscale Model of Nanocrystals | Nanovoids in Grain Boundary | Micro- to Meso -Fracture | Fracture of Thin Bodies | Elastic Damage to Crack | Ductile Gurson-Thomason Damage to Crack | Smart Composite Materials | Failure of Polycrystalline Films | Kirchhoff-Love Shells |
Research
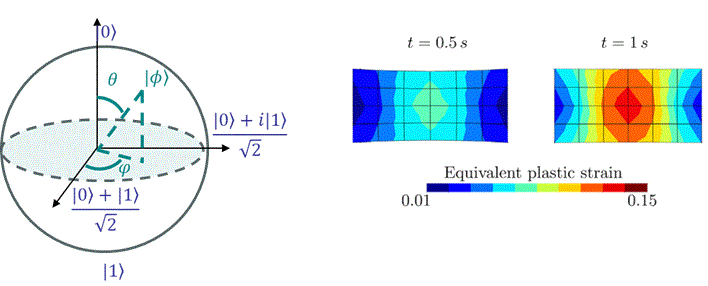
Quantum Computing
Deep Material Networks from the interactions viewpoint
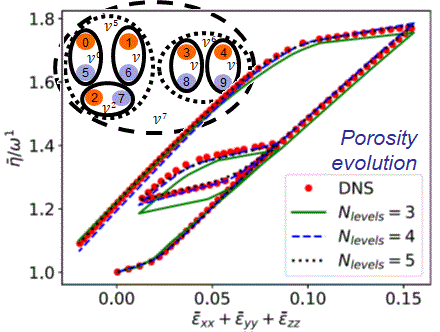
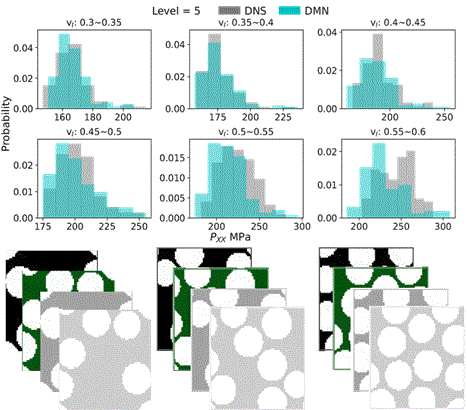
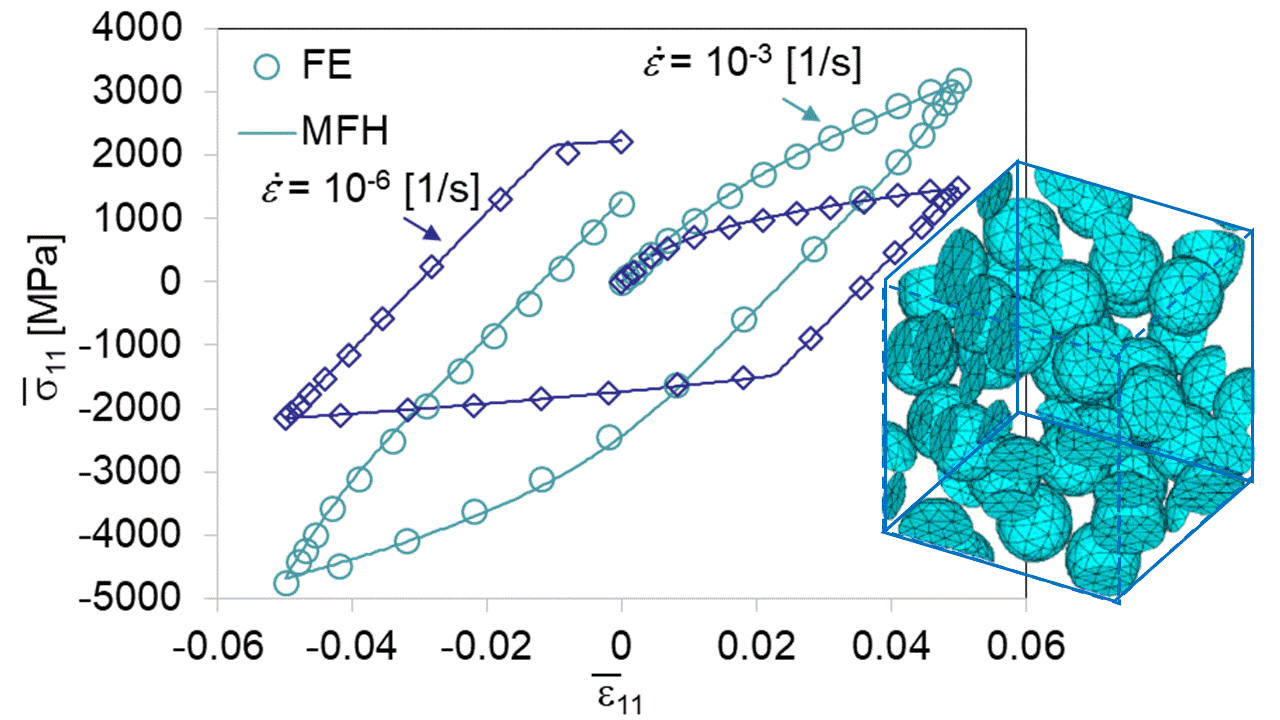
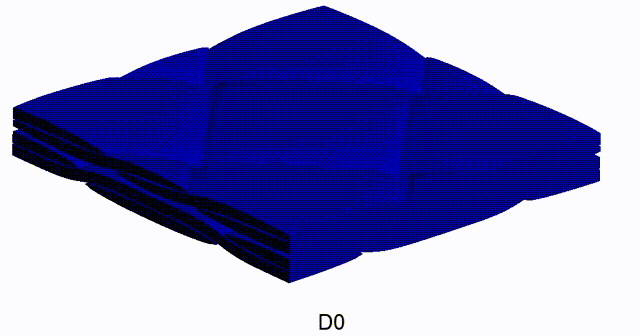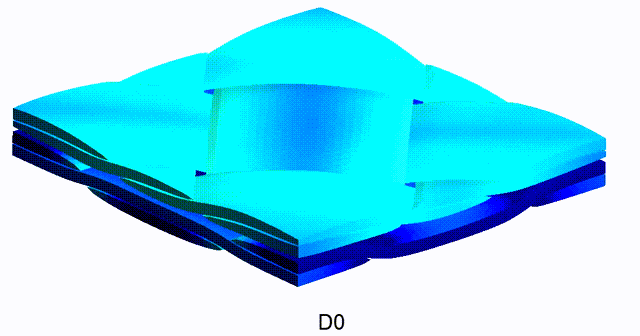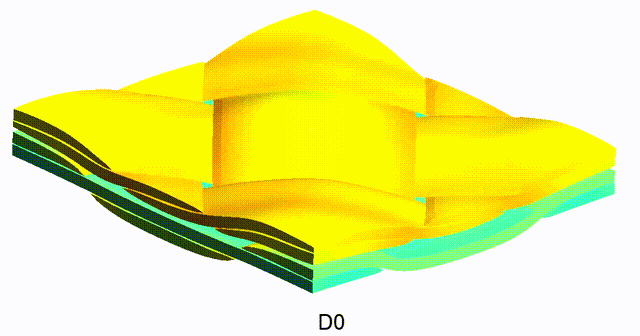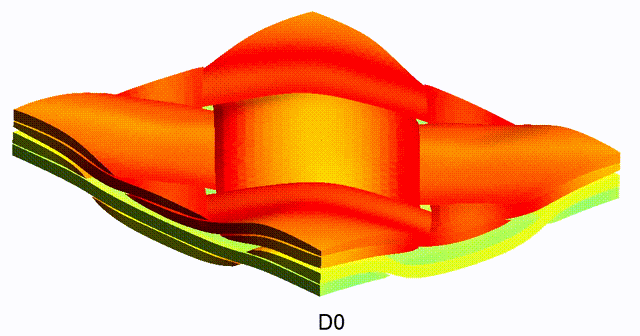
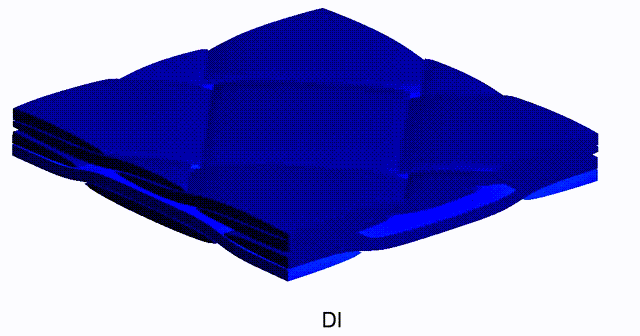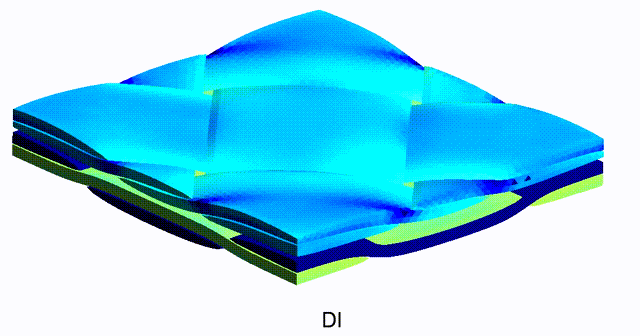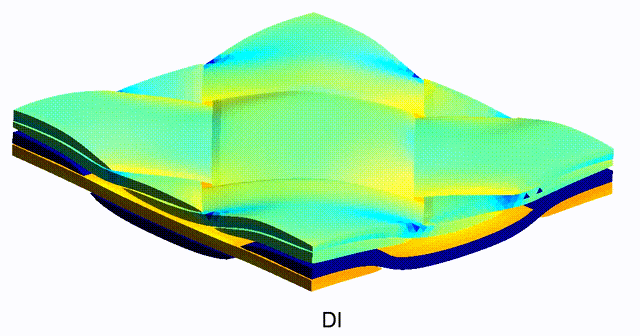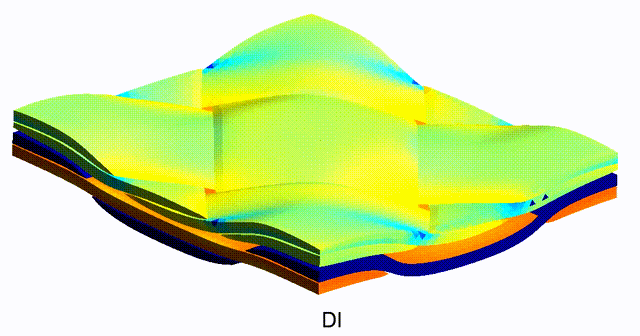
Mean-Field-based Deep Material Networks for woven composites
Stochastic Deep Material Network
Data-driven multi-scale methods
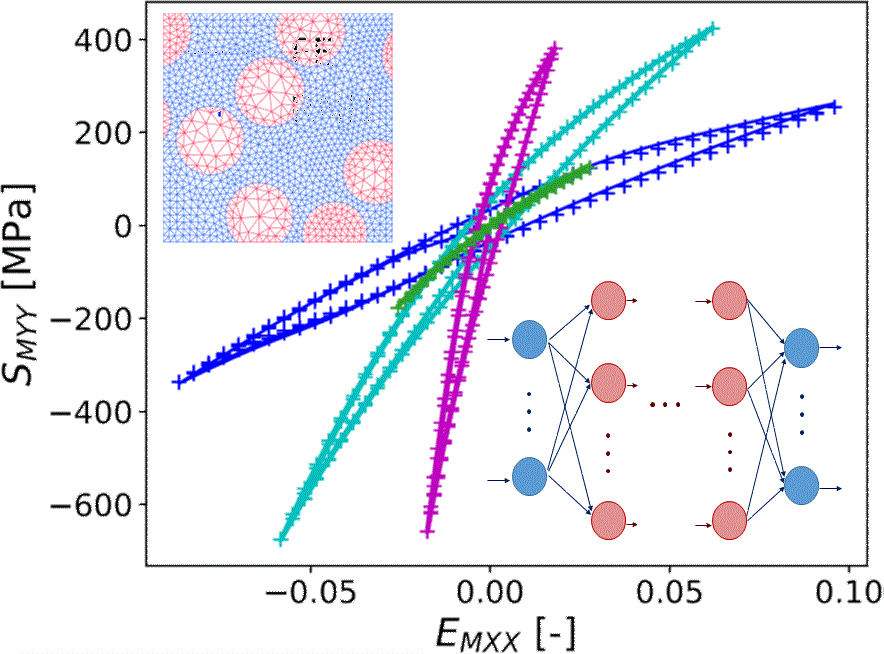
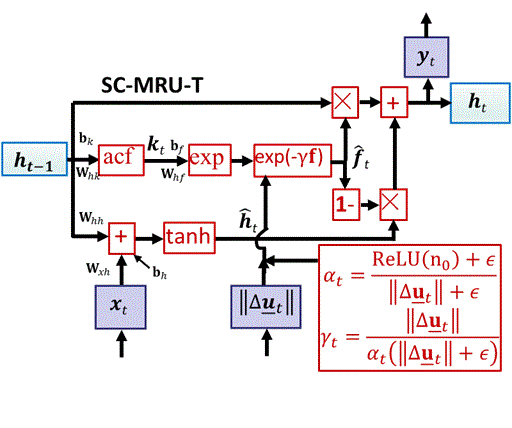
Self-Consistent Recurrent Neural Network
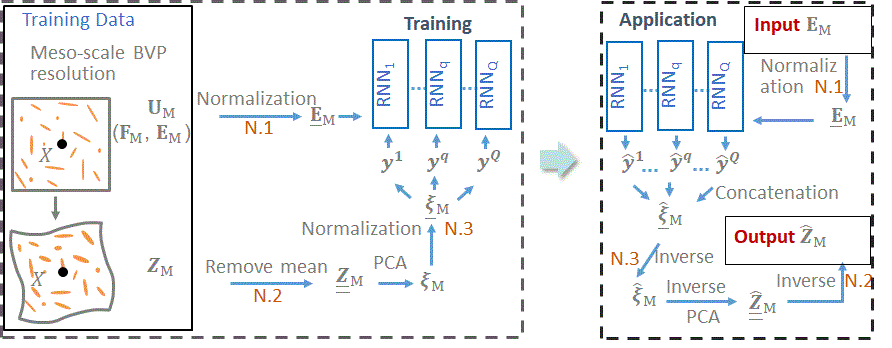
Recurrent Neural Networks with dimensionality reduction and breakdown
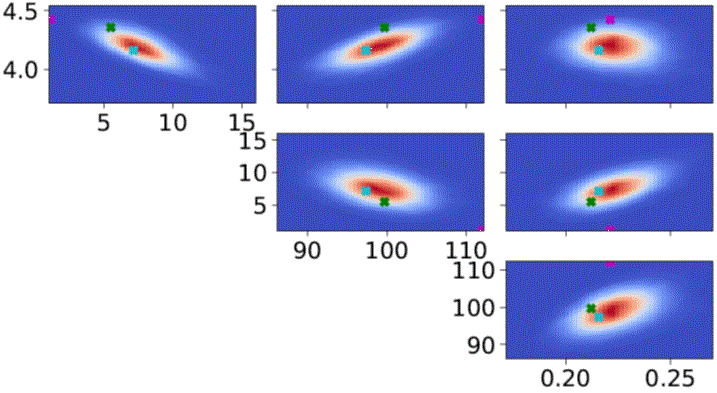
Sequential Bayesian Inference of complex model parameters & Bayesian inference of multi-scale model parameters
Shear & Necking-coalescence for porous models
Ductile failure of high entropy alloys
Microstructural reinforced highly crosslinked epoxy analysis
Finite-strain thermomechanical quasi-nonlinear-viscoelastic viscoplastic model for thermoplastics
Instabilities Across the Scales: Computational Homogenization of Cellular Material Buckling
Second order homogenization without RVE size effect: Computational Homogenization of metamaterials
Incremental-secant Mean-Field-Homogenization for elasto-visco-plastic composite materials
Non-Local Damage-Enhanced Mean-Field-Homogenization for Composite Laminates
Non-Local Damage & Phase Field-Enhanced Mean-Field-Homogenization for Laminates & Woven Composites
Stochastic Homogenization of Composite Materials
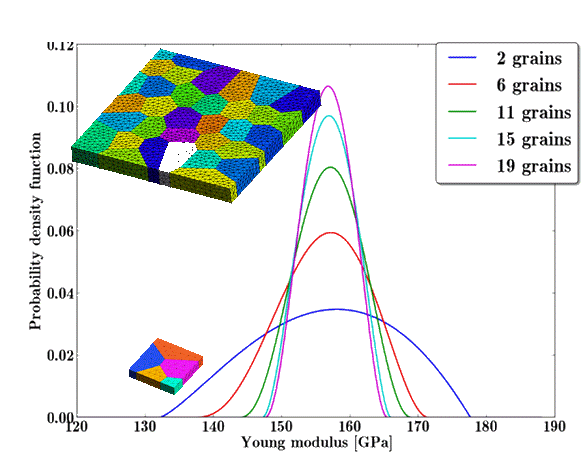
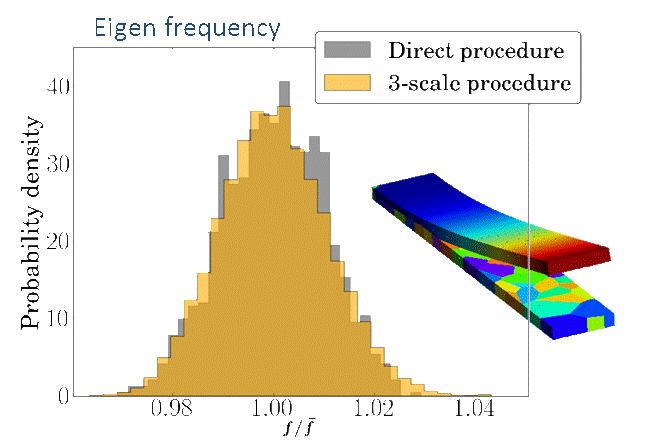
Stochastic 3-Scale Method for Polycrystalline Materials
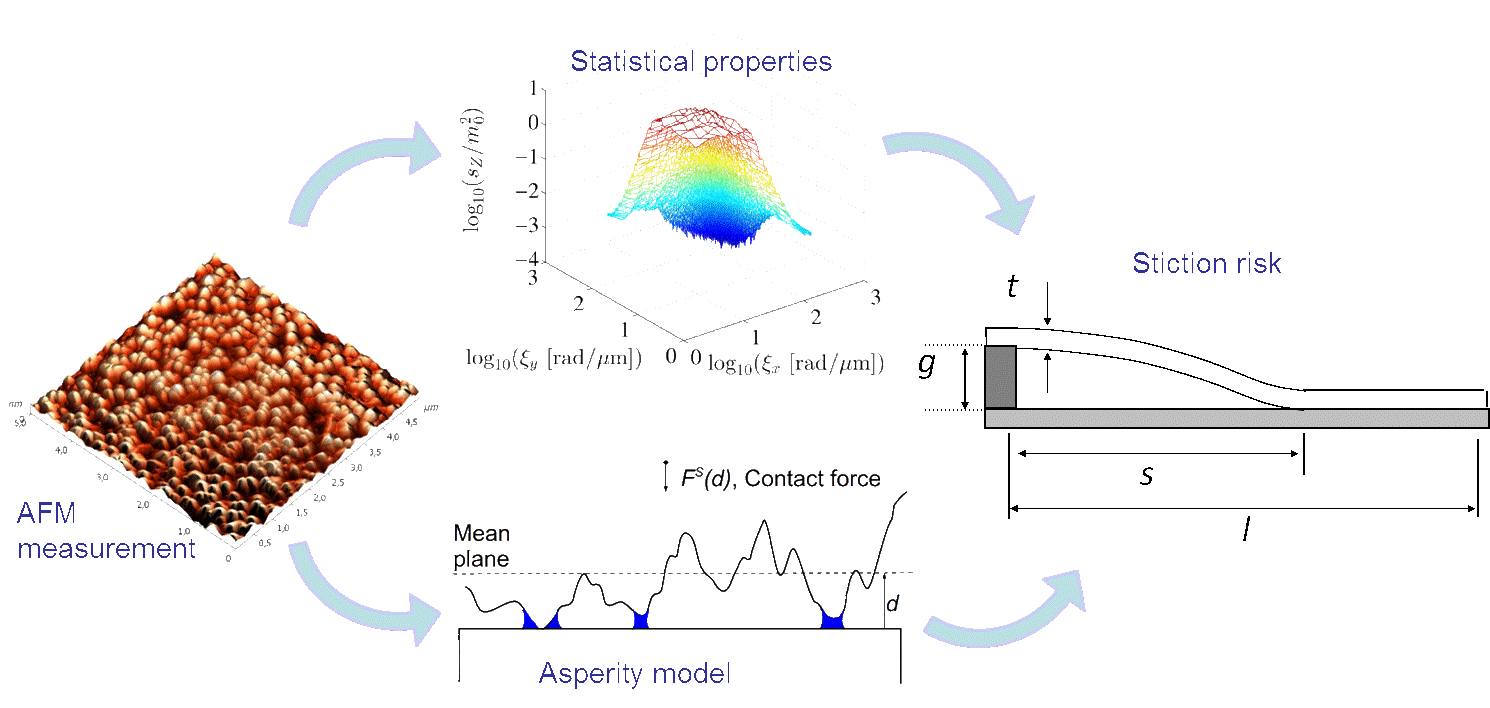
Stochastic Models for the Stiction Risk Prediction in MEMS
Link to CM3 slides
Multiscale Model of Nanocrystal Grain Boundary Sliding
Effect of Nanovoids in Grain Boundary Sliding
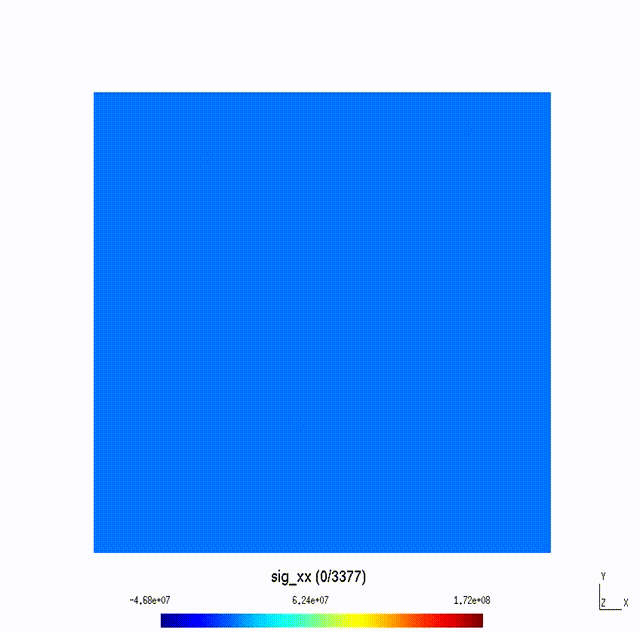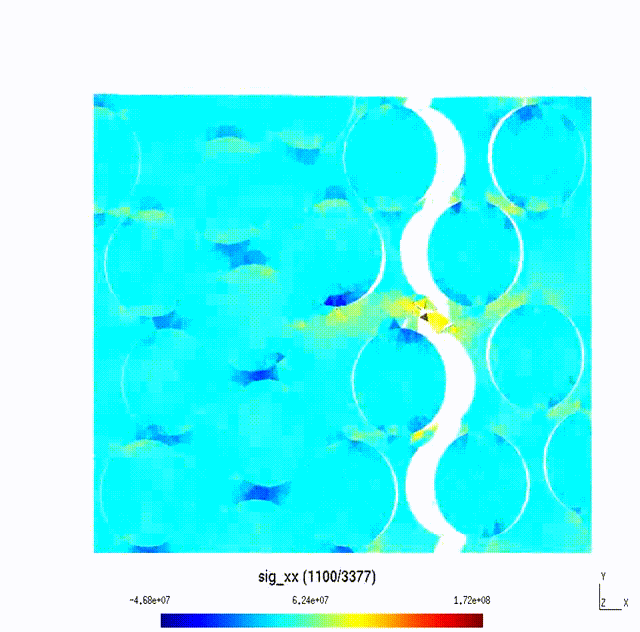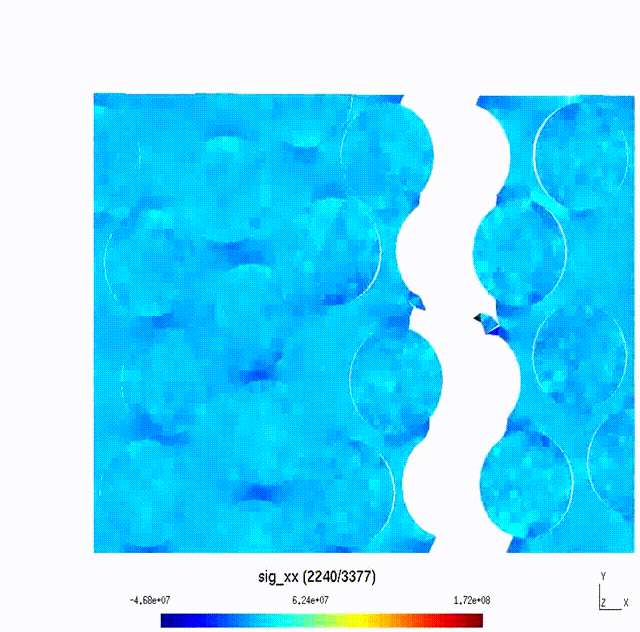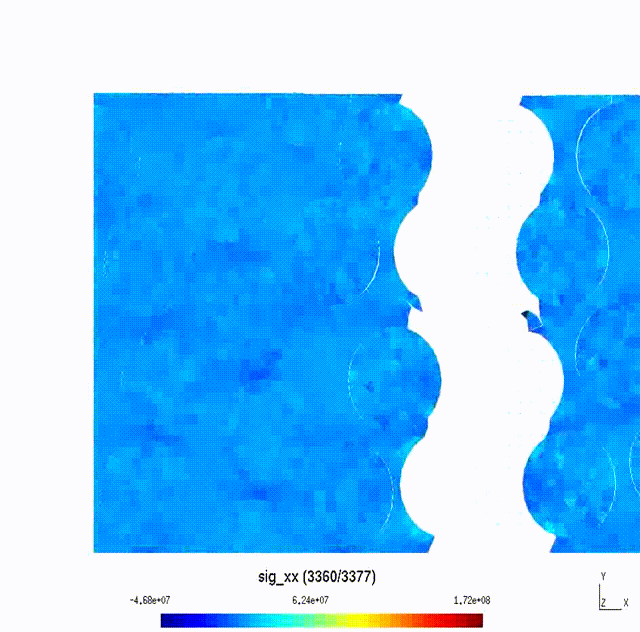
Micro-Scale to Meso-Scale Fracture of Composite Materials
Consistent Numerical Framework for the Fracture of Thin Bodies
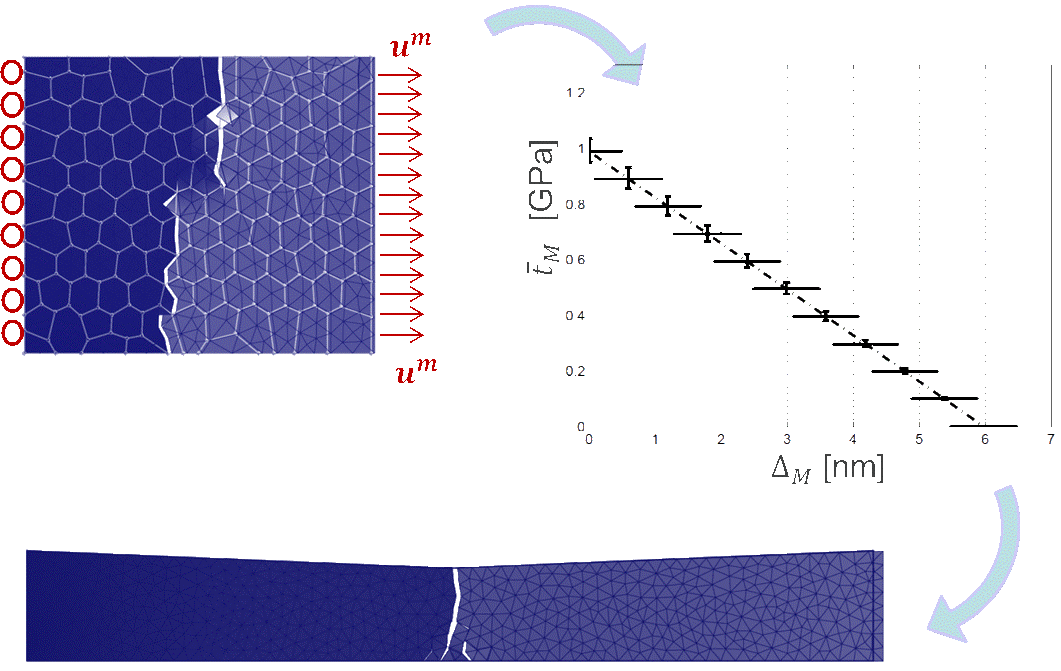
Consistent Elastic Damage to Crack Transition
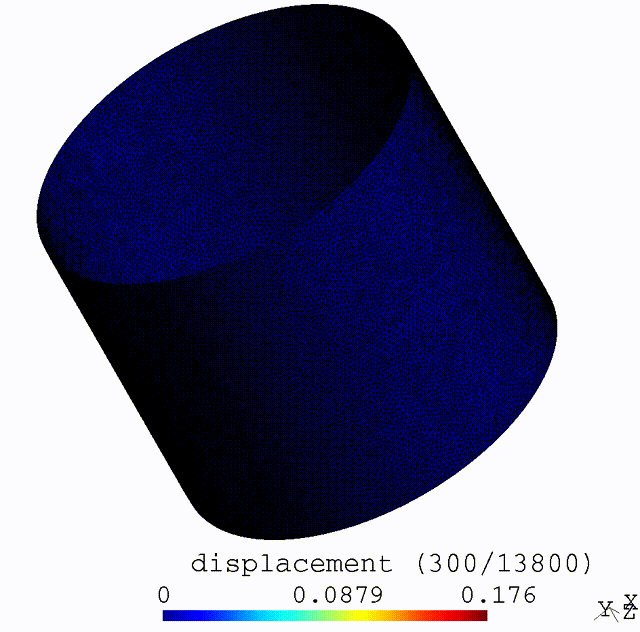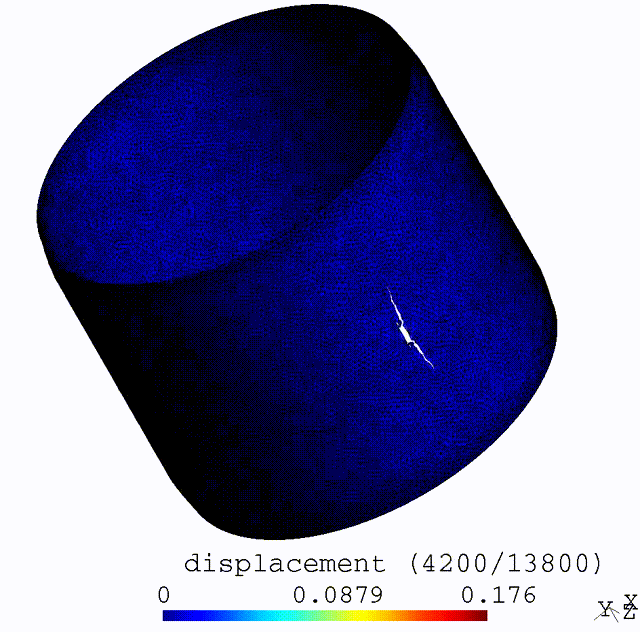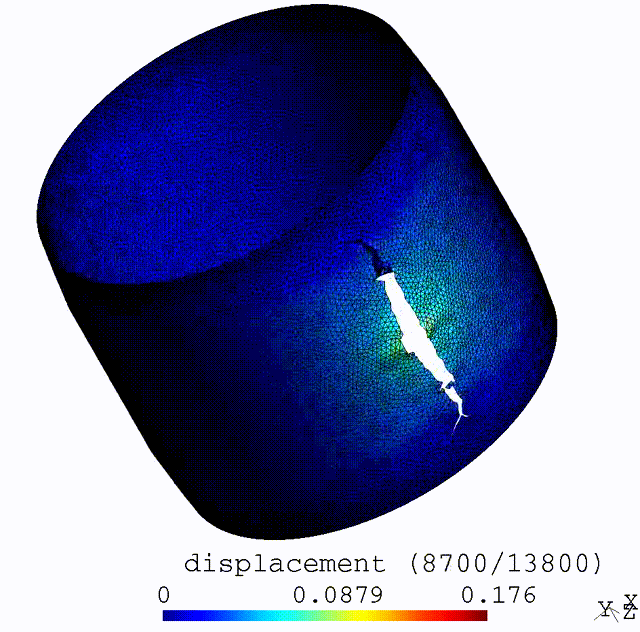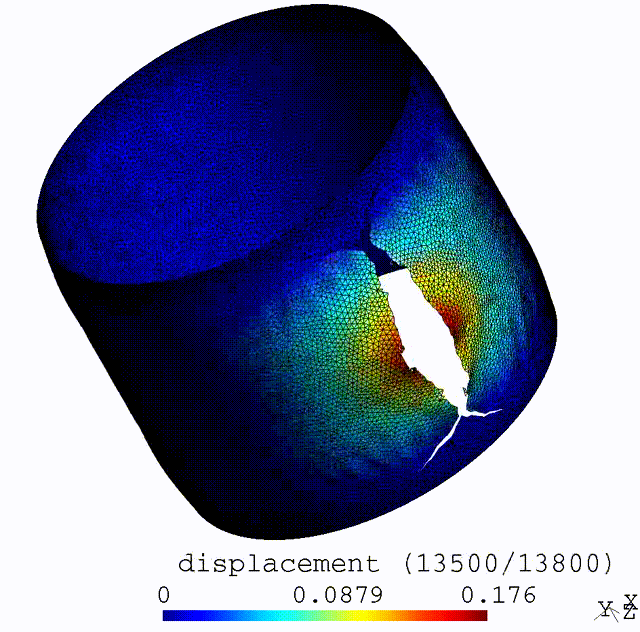
Ductile Gurson-Thomason Damage to Crack Transition
Smart Composite Materials
Multi-Scale Failure of Polycrystalline Films
Kirchhoff-Love Shells without Rotational Degrees of Freedom
E-mail: L.Noels @ ulg.ac.be; Address: University of Liège, CM3 B52, Allée de la découverte 9, B4000 Liège, Belgium