SIF Computation >SIF Handbooks (LEMF)
Solutions of crack problems for plates of finite dimensions are tabulated in handbooks. The solutions are obtained by different means (analytical, numerical, ...) for different crack lengths.
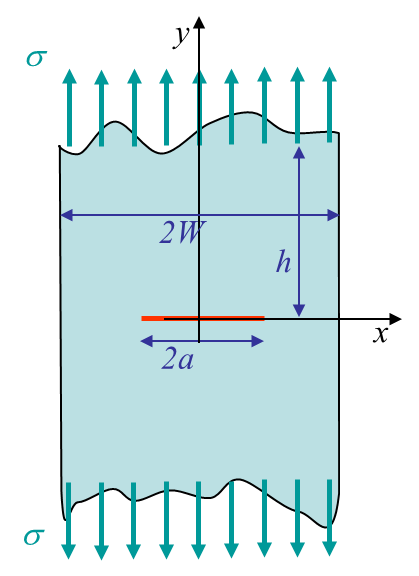
As an example we report here a method for the problem of a centered crack of size $2a$ loaded in mode I in a plate of width $2W$, see Picture IV.13, under the condition $h/W>3$. The resolution method reads
- The general formula reads
\begin{equation} K_I = \sigma \sqrt{\pi a}\; f\left(\tfrac{a}{W}\right)\,.\label{eq:SIFIsida1}\end{equation} - The function $f\left(\tfrac{a}{W}\right)$ can be obtained by different resolution methods, leading to different accuracies.
Some of the possible solutions for the function $f\left(\tfrac{a}{W}\right)$ are tabulated here below
- Using the periodic crack approximation
\begin{equation} f\left(\tfrac{a}{W}\right)=\sqrt{\frac{2W}{\pi a}\tan{\frac{\pi a}{2W}}}\end{equation}- <5% error for $a/W<0.5$;
- Irwin, 1957.
- Using Laurent series expansion
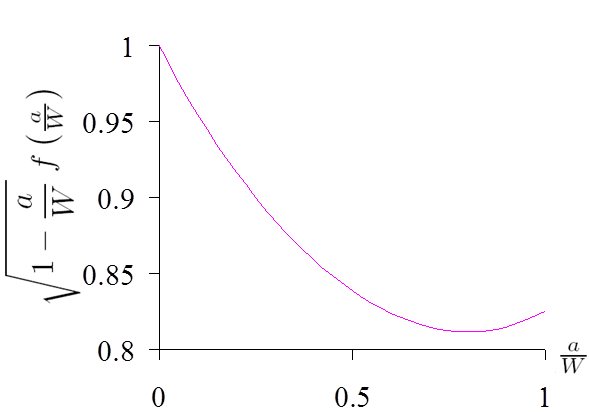
- Solution reported in Picture IV.14;
- Practically exact up to $a/W=0.9$;
- Isida, 1973.
- Fitting Isidia's values
\begin{equation}f\left(\tfrac{a}{W}\right)=\left[ 1-0.025\left(\tfrac{a}{W}\right)^2+ 0.06\left(\tfrac{a}{W}\right)^4\right]\sqrt{\frac{1}{\cos{\frac{\pi a}{2 W}}}}\end{equation}
- <0.1% error;
- Tada, 1973.