\(\newcommand{\cauchy}{\boldsymbol{\sigma}}\) \(\newcommand{\strain}{\boldsymbol{\varepsilon}}\) \(\newcommand{\uV}{\boldsymbol}\) \(\newcommand{\uT}{\boldsymbol}\) \(\newcommand{\defu}{\boldsymbol{u}}\)
The $J$-integral
This chapter covers the methodologies developed to evaluate the $J$-integral, which was shown to be of importance in non-linear fracture models such as in the HRR theory. Indeed, in elasto-plasticity, the $J$-integral characterizes the crack tip loading, and thus can be used to evaluate failure onset and, under some assumptions, the tearing properties, i.e. the resistance curve during crack growth.
$J$-integral > HRR theory (continuation)
The understanding of the HRR theory is essential to understand the practical use of the $J$-integral theory. The related theory is described in the beforehand chapter.
$J$-integral > Application for elasto-plastic materials
Irreversibility vs. reversibility

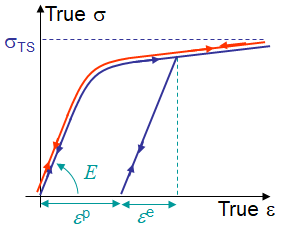
Let us consider two cracked samples, see Picture IX.1, made of two different materials exhibiting the apparent same behavior during proportional and monotonic loading:
- Sample 1, in red, is made of an elastic (and thus reversible) non-linear material as illustrated in Picture IX.2. For a reversible material, an internal potential exists, and the energy release rate $G$ can be defined. If the crack growths straight ahead, we thus have $G_1=J_1$ as previously demonstrated.
- Sample 2, in blue, is made of an elasto-plastic (and thus irreversible) material, which exhibits the same stress-strain response than the elastic material during proportional monotonic loading, as illustrated in Picture IX.2.
Therefore, in the absence of crack propagation, the two samples have the same stress distributions with $G_2=G_1$ and $J_2=J_1$. As a result $J_2=G_2$ for elasto-plasticity at the conditions, on the one hand, that the loading remains proportional and monotonic (i.e. there is no crack propagation) and, on the other hand, that the crack will subsequently growth straight ahead.
The interest in evaluating the $J$-integral for a given cracked body configuration is thus high in elasto-plasticity since it allows
- Experimentally determining the critical $J_C=G_C$ at which a crack propagates;
- Assessing the crack propagation for a given configuration.
Evaluation of the $J$-integral
In the following we will thus be interested, on the one hand on how to evaluate the $J$-integral:
- Using a numerical approach;
- Using energetic methods;
- Using experimental methods;
- Using engineering methods derived from the latter ones;
and, on the other hand, on how to experimentally evaluate the critical $J_C$:
- For crack initiation to define the toughness;
- During crack propagation (when proportional loading assumption remains valid) to define the resistance curve $J_R(\Delta a)$ of ductile materials.