\(\newcommand{\cauchy}{\boldsymbol{\sigma}}\) \(\newcommand{\strain}{\boldsymbol{\varepsilon}}\) \(\newcommand{\uV}{\boldsymbol}\) \(\newcommand{\uT}{\boldsymbol}\) \(\newcommand{\defu}{\boldsymbol{u}}\)
HRR theory > Validity of HRR field
Lastly, we want to discuss the validity and applicability of the HRR solution for different loading intensities.
Small Scale Yielding (SSY) case
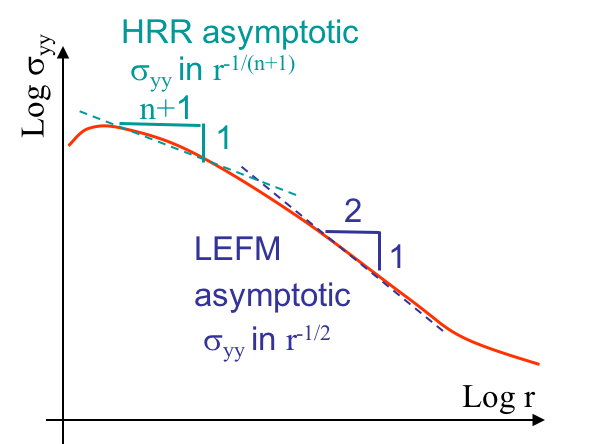
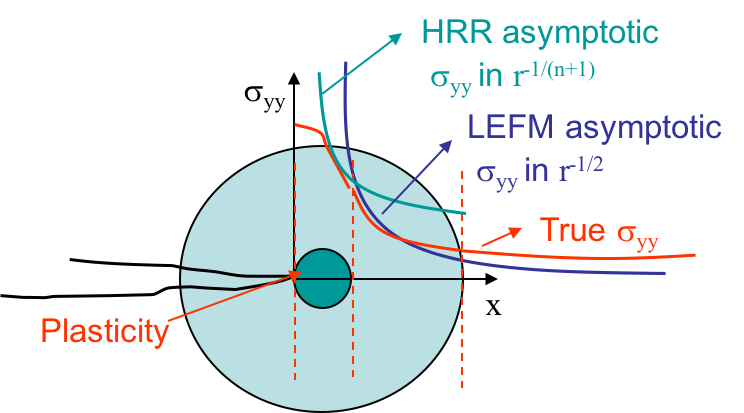
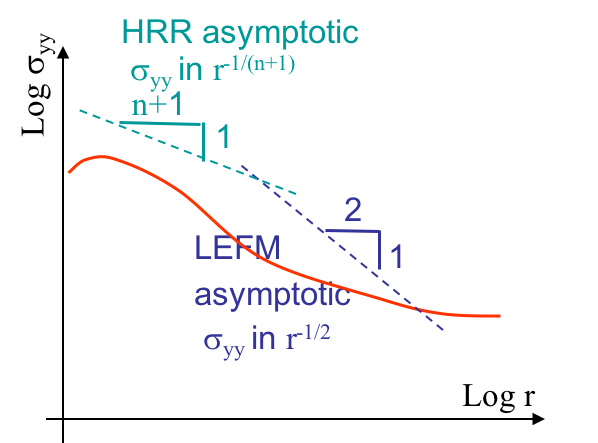
Assuming the process zone remains confined at crack tip and that a $K$-dominance zone develops, we are under Small Scale Yielding (SSY). In that case, there exists a zone, in light green in Picture VIII.35, in which the behavior is elastic and in which the asymptotic solution of the LEFM governed by the SIF $K$ holds. Outside this zone, since the solution is asymptotic, the structural loading is not captured. When getting closer to crack tip, we are entering the process zone, and the LEFM asymptotic solution is no longer valid. However, there is a part of the process zone in which the asymptotic HRR solution governed by the $J$-integral is valid and matches the real behavior. However, contrarily to the real behavior, the asymptotic HRR solution is singular at crack tip. There are thus two separate regions in which one of the two asymptotic solutions captures the evolution of the stress with the radius $r$, as illustrated in the log-scales. Fracture can thus be predicted using either the SIF or the $J$-integral.
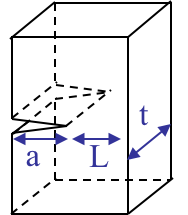
Practically, the SSY condition is satisfied if the crack length $a$, the ligament $L$, see Picture VIII.37, but also the thickness if we want to avoid the thickness dependency on the toughness, are all larger than 25 times the plastic zone length $r_p$, that is in plane-$\varepsilon$ state
\begin{equation} a,\,t,\,L > 25 r_p \simeq \frac{25}{3\pi}\left(\frac{K_I}{\sigma_p^0}\right)^2\simeq 2.5 \left(\frac{K_I}{\sigma_p^0}\right)^2 \, \text{.} \label{eq:SSYcond}\end{equation}
Since both HRR and LEFM asymptotic solutions hold, the crack initiation criterion can be based on $J$ or $\delta_t$ such as $J \geq J_C$ or $\delta_t \geq \delta_C$. But as the LEFM solution holds, we can still use $K\left(a\right) \geq K_C$ which might be corrected by using the effective length $a_{eff}$ if $\sigma_{\infty} < 50\%$ of $\sigma_p^0$.
When considering a toughness test or a crack propagation assessment, Eq. (\ref{eq:SSYcond}) becomes
\begin{equation} a,\,t,\,L > 2.5 \left(\frac{K_C}{\sigma_p^0}\right)^2 \, \text{.} \label{eq:SSYKC}\end{equation}
To provide some material examples for which the validity in SSY is ensured or not, a titanium alloy is compared to a mild steel:
- Titanium alloy 6%Al-4%V
- Yield stress: $\simeq$ 830 MPa;
- Toughness: $\simeq$ 55 MPa m$^{1/2}$;
- So Eq. (\ref{eq:SSYKC}) becomes $a$, $t$, $L$ $>$ 1.1 cm;
- Mild steel
- Yield stress: $\simeq$ 350 MPa;
- Toughness: $\simeq$250 MPa m$^{1/2}$;
- So Eq. (\ref{eq:SSYKC}) becomes $a$, $t$, $L$ $>$ 1.27 m !!!
For a toughness test to be valid, all three dimensions, i.e. $a$, $t$, $L$, have to be larger than 1.1 cm for the titanium alloy. On the other hand, for the steel, the critical length rises to 1.27 m which cannot be practically achieved.
Elasto-plastic small deformation case
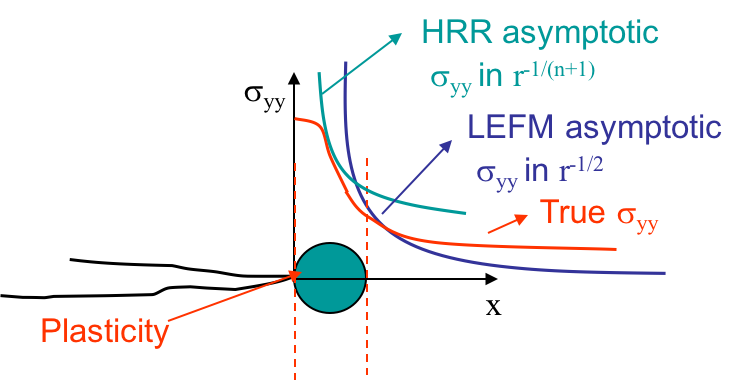
When elasto-plasticity develops further from the crack tip, but still assuming that the deformations are small, the zone of $K$-dominance no longer exists. Nevertheless, we still have one zone of $J$-dominance, part of the dark green zone in Picture VIII.37, in which the asymptotic HRR solution is valid, see Picture VIII.38. The asymptotic solution of the LEFM is NOT valid in the elastic zone, as this one is now located further from the crack tip so that the structural loading cannot be neglected.
The conditions to have $J$-dominance zone are that all sizes are 25 larger than the crack tip opening displacement (CTOD), i.e.
\begin{equation} a,\,t,\,L > 25 \delta_t\simeq 25 \frac{J}{\sigma_p^0} \, \text{.} \label{eq:HRRcond}\end{equation}
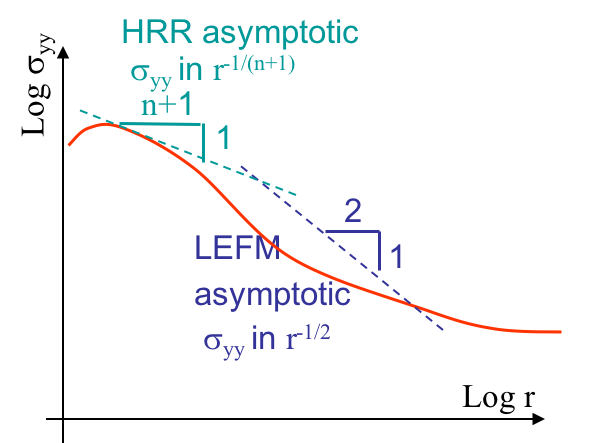
Once again, similar to SSY, the crack initiation criteria based on $J$ or $\delta_t$ such as for $J \geq J_C$ or $\delta_t \geq \delta_C$ are valid. $J$ and $\delta_t$ depend among others on the crack length $a$, the geometry and the loading. A main difference to SSY is that the LEFM solution DOES NOT hold since there is no $K$-dominance zone, and hence, we CANNOT use $K\left(a\right) \geq K_C$.
The toughness of a material should thus be evaluated though the $J$-integral in which case Eq. (\ref{eq:HRRcond}) becomes
\begin{equation} a,\,t,\,L > 25 \frac{J_C}{\sigma_p^0} \, \text{.} \label{eq:HRRJC}\end{equation}
Let us have a look again at the two previously considered materials to have an estimation of the crack sizes so that the HRR field is valid in the elasto-plastic conditions.
- Titanium alloy 6%Al-4%V
- Yield stress: \simeq 830 MPa;
- Toughness: \simeq 55 MPa m$^{1/2}$;
- Young's modulus: \simeq 110 GPa;
- So Eq. (\ref{eq:HRRJC}) \becomes $a$, $t$, $L$ $>$ 0.75 mm;
- Mild steel
- Yield: \simeq 350 MPa;
- Toughness: \simeq 250 MPa m$^{1/2}$;
- Young's modulus: \simeq 210 GPa;
- So Eq. (\ref{eq:HRRJC}) becomes $a$, $t$, $L$ $>$ 1.93 cm.
We can observe that when measuring the critical $J_C$ instead of $K_C$ (which can be deduced from $E' J_C=K_{IC}^2$), the limit for the crack sizes decreases for both materials to a reasonably small value. So for ductile material, the toughness $K_C$ cannot be measured experimentally, and is deduced from ameasured $J_C$.
Large scale yielding case
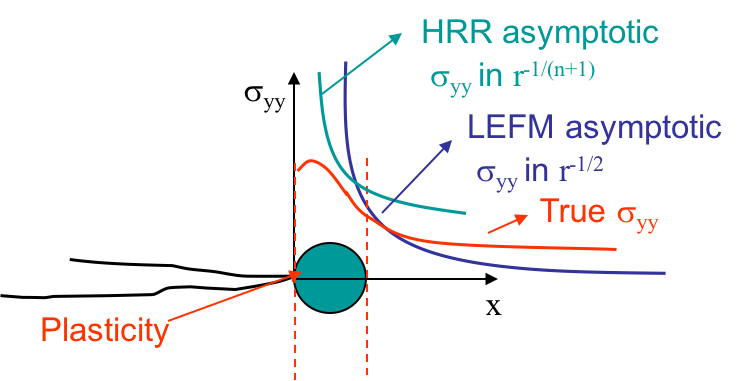
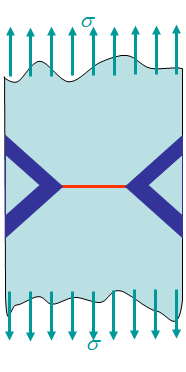
Lastly, if the loading conditions keep increasing in amplitude, or if the ligament is too small, large plastic deformations arise. In such a case, the small deformations assumption does not hold and neither the HRR field nor the LEFM asymptotic field are valid. This is illustrated in Picture VIII.40 or Picture VIII.41 where it can be seen that the asymptotic solutions are nowhere in agreement with the true stress field. For large scale yielding, defining a criterion for the crack initiation is not an easy task as there is no zone of $J$-dominance. The question arises whether we can still use $J$ or not?
Actually, the plastic strain concentrations depend on the experiment which might be of the forms depicted in Picture VIII.43 to Picture VIII.44. It appears that the plastic zones are not reproducible from one test to another. Regarding the crack initiation criterion, we can say that the solution is no longer uniquely governed by $J$. The relation between $J$ and $\delta_t$ is dependent on the configuration and on the loading. The critical $J_C$ measured for an experiment might not be valid for another one. A two-parameter characterization is thus required.